Passa ai contenuti principali

TUTORIAL FUNZIONI: come rappresentarle / controllare grafici

In questa breve guida ti spiegherò come rappresentare una funzione con alcuni strumenti informatici gratuiti o di largo uso: questo può esserti molto utile se devi, ad esempio, controllare di aver rappresentato correttamente una funzione dopo averla studiata analiticamente.

WolframAlpha

Si tratta di uno strumento parzialmente gratuito disponibile online e anche tramite app. La parte disponibile gratuitamente del sito di solito è più che sufficiente: se vuoi rappresentare il grafico di una funzione basta inserirne l'espressione analitica nella forma f(x)=... oppure anche y=... . Tale strumento accetta anche funzioni di due variabili, che rappresenta tramite una superficie. Inoltre navigando nelle varie parti del sito è possibile utilizzare una serie di widget gratuiti per risolvere molti problemi: derivate, integrali, equazioni differenziali... insomma: l'ho presentato per primo non certo a caso!
Se poi volete di più, potete sempre acquistare la versione a pagamento: di certo non sono soldi spesi male, ma dipende sempre quanto desiderate da quell'applicazione. Per controllare se il grafico di una funzione è coerente o no con quanto abbiamo calcolato "carta e penna", la versione gratuita basta e avanza. Link:

GeoGebra

Ha moltissime funzioni e si può utilizzare sia come calcolatrice grafica disponibile online gratuitamente, sia come programma basato sul PC dell'utente: consente di rappresentare grafici di funzioni esattamente come in WolframAlpha, ma anche di trovare l'intersezione tra grafici di diverse funzioni o altri elementi definiti nel programma. Risulta molto utile anche per lo studio della geometria piana e consente inoltre di svolgere analisi parametriche sulle funzioni usando, ad esempio, gli "slider". Di seguito i link:

MS Excel / OpenOffice Calc

Si tratta di fogli di calcolo adatti agli scopi più disparati: organizzazione turni di lavoro, calcolo di scorte a magazzino in azienda... e anche, perché no, disegno di grafici di funzioni. MS Excel non è normalmente disponibile gratuitamente ma fa parte della suite di Microsoft Office: spesso tali strumenti possono essere messi a disposizione anche gratuitamente ad esempio dalle università o da alcuni enti per i propri studenti/addetti...sennò c'è sempre la controparte open source, cioè OpenOffice-Calc. I comandi da fornire per disegnare il nostro grafico sono assolutamente identici tra i due programmi: si genera una colonna di valori ordinati (le nostre x dove vogliamo studiare la funzione) e si impone al programma che un'altra colonna (y) prenda in entrata i valori della prima, restituendo, per ogni riga della prima colonna, un valore di y calcolato con la formula della nostra funzione. In pratica è come se ci mettessimo a calcolare la funzione a mano in un certo numero di punti e poi rappresentassimo il grafico collegando i punti. 

esempio
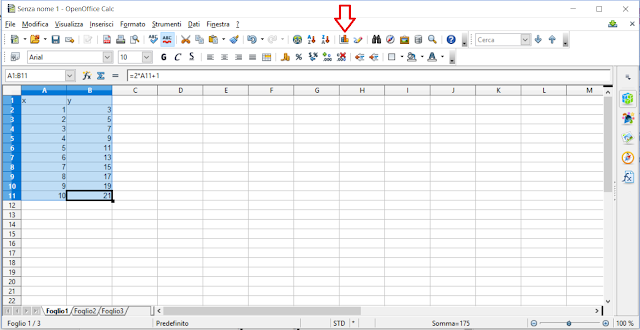
vogliamo rappresentare y=f(x)=2x+1 tra x=0 e x=10 con un passo di calcolo pari a 1
Definiamo la colonna delle x (basta scrivere i primi due valori della colonna, selezionarli e trascinare verso il basso il quadratino che compare in basso a destra nella selezione):


Ora definiamo che valore dovrà assumere la prima cella della colonna delle y. Per introdurre una funzione, Calc ed Excel richiedono di introdurla usando " = "


Quando abbiamo finito di scrivere, premiamo INVIO. La cella in cui abbiamo scritto la funzione assumerà un valore (nel nostro caso f(1)=2*1+1=3 ). Per calcolare anche tutti gli altri valori dobbiamo riscrivere ogni volta la funzione? NO! Basta selezionare la prima cella in cui abbiamo scritto la funzione e trascinare verso il basso la il quadratino in basso a destra
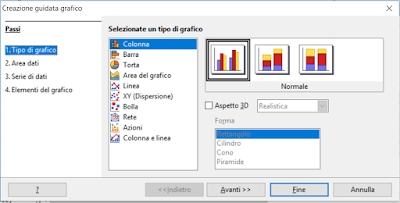
Quindi ora abbiamo tutti i valori di x e y che ci servono, usiamo un grafico per rappresentarli: selezioniamo le due colonne e clicchiamo sull'icona indicata in rosso


e nella finestra di dialogo che si apre 

scegliamo "XY (Dispersione)" e dal successivo menù "punti e linee". Otteniamo


che è il grafico della nostra funzione. 
NOTA BENE: per funzioni semplici, prive di discontinuità e asintoti, l'approssimazione sarà molto buona, però, se si desidera studiare approfonditamente una funzione in cui ci sono criticità, meglio ricorrere ai primi due strumenti. 

Link:

Matlab/Octave

Dulcis in fundo troviamo un software che è sicuramente una pietra miliare del calcolo scientifico, tuttavia presenta due scogli per l'utente inesperto: 
  1. è necessario avere solide basi di programmazione per potersi districare in questo programma
  2. Matlab è a pagamento, anche se esistono versioni gratuite per gli studenti di istituti convenzionati, sennò c'è sempre la controparte open source, cioè Octave. Anche qui, questi due programmi condividono linguaggi molto simili per la maggior parte delle funzioni.
Per quanto riguarda la rappresentazione di funzioni, il sito di Mathworks fornisce guide assolutamente di ottimo livello e ricche di esempi, dunque rimando direttamente al sito:

In generale Matlab è sicuramente lo strumento più potente che abbia presentato in questa guida: la sua utilità è decisamente ben oltre quanto qui ho voluto presentare.

Commenti

Posta un commento

Post popolari in questo blog

ESERCIZI RISOLTI sulle FUNZIONI: iniettività, suriettività, biiettività

In questo articolo ti presenterò una serie di esercizi risolti su come si determina quando una funzione è iniettiva, suriettiva o biiettiva. Non ti ricordi questi termini? Leggi la mia guida  FUNZIONI esercizio 1 Si determini se la funzione f(x)=2x+1 è biiettiva. ----- Per dimostrare che la funzione in oggetto è biiettiva, sarà necessario dimostrare che è SIA iniettiva, SIA suriettiva . Iniziamo con l'iniettività . Ricordiamoci che " Una funzione  f(x)  è INIETTIVA se PER OGNI  x,x ' diversi tra loro, le loro immagini sono diverse ovvero  f(x)  è diverso da  f(x') ." Dunque per dimostrare che una funzione è iniettiva, dobbiamo dimostrare che lo è PER OGNI scelta di x e x' (cioè per qualsiasi x, x'), mentre per dire che una funzione non è iniettiva, sarà sufficiente trovare un controesempio, ovvero trovare un x e un x' tale che se x e x' sono diversi, f(x)=f(x'). Dimostriamo quindi che la funzione è iniettiva: Supponi...
1 commento
Continua a leggere

VERSIONE GRECO: Una madre spartana (Diodoro Siculo)

TRADUZIONE: Gli Ateniesi, dopo aver recuperato e seppellito i cadaveri con una tregua(lett: cadaveri che erano garanzia di tregue), salparono alla volta di Atene. Dopo che alcuni erano giunti a Sparta dalla battaglia e dopo che avevano annunciato la vittore e contemporaneamente la morte di Brasida, la madre di Brasida, quando venne a sapere ciò che era stato fatto durante la battaglia, chiese chi fosse stato nello schieramento di Brasida; quando essi risposero che (Brasida) era stato il migliore degli Spartani, la madre del morto disse che suo figlio Brasida era un uomo nobile, anche se (era) (lett: eppure) più povero di molti altri. Dopo che queste parole si erano diffuse per la città, gli efori onorarono pubblicamente la donna, poiché anteponeva la lode della patria alla gloria del figlio.
Posta un commento
Continua a leggere

VERSIONE GRECO: Pillole di saggezza(Isocrate)

TRADUZIONE In primo luogo, dunque, osserva i doveri religiosi non solo facendo sacrifici(per gli dei), ma anche restando fedele ai giuramenti; quello, infatti, è segno di benessere economico( lett: della disponibilità di denaro), questo, invece, è testimonianza della nobiltà dei modi. Onora sempre la divinità, soprattutto insieme alla città; così, infatti, sembrerà che tu fai sacrifici per gli dei e che, contemporaneamente, osservi le leggi. Nei confronti dei figli sii come potresti desiderare che fossero i tuoi figli nei tuoi confronti( lett: sii tale quali potresti desiderare che fossero i tuoi figli nei tuoi confronti). Tra gli esercizi fisici( lett: relativamente al corpo), esegui non quelli per (sviluppare) la forza, ma quelli per (sviluppare) la salute; [...] ritieni sia adatta a te al massimo grado moderazione, pudore, giustizia e saggezza; infatti il comportamento dei giovani sembra essere retto da tutte queste virtù. Augurati di non dover mai nascondere nulla di turpe avendol...
Posta un commento
Continua a leggere